MULTIPLYING NEGATIVE NUMBERS

Multiplying Negative Numbers

Definition:

If A and B are positive numbers then we can define 

A x-B = -(AxB)

Concept Meaning:

When We Multiply:

			Example
×	two positives make a positive:		3 × 2 = 6
×	two negatives make a positive:		(−3) × (−2) = 6
×	a negative and a positive make a negative:		(−3) × 2 = −6
×	a positive and a negative make a negative:		3 × (−2) = −6

Yes indeed, two negatives make a positive, and we will explain why, with examples!

Signs

Let's talk about signs.
"+" is the positive sign, "−" is the negative sign.
When a number has no sign it usually means that it is positive.

Example: 5 is really +5

And we can put () around the numbers to avoid confusion.

Example: 3 × −2 can be written as 3 × (−2)

Two Signs: The Rules

"Two like signs make a positive sign, two unlike signs make a negative sign"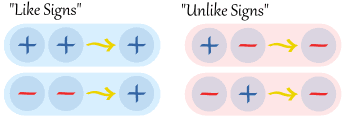

Example: (−2) × (+5)

The signs are − and + (a negative sign and a positive sign), so they are unlike signs (they are different to each other)
So the result must be negative:

(−2) × (+5) = -10

Example: (−4) × (−3)

The signs are − and − (they are both negative signs), so they are like signs (like each other)
So the result must be positive:

(−4) × (−3) = +12

Why does multiplying two negative numbers make a positive?

Well, first there is the "common sense" explanation:

When I say "Eat!" I am encouraging you to eat (positive)
But when I say "Do not eat!" I am saying the opposite (negative).
Now if I say "Do NOT not eat!", I am saying I don't want you to starve, so I am back to saying "Eat!" (positive).

So, two negatives make a positive, and if that satisfies you, then you don't need to read any more.

 Teaching Resources:

Direction

It is all about direction. Remember the Number Line?

Well here we have Baby Steven taking his first steps. He takes 2 paces at a time, and does this three times, so he moves 2 steps x 3 = 6 steps forward:

Now, Baby Steven can also step backwards (he is a clever little guy). His Dad puts him back at the start and then Steven steps backwards 2 steps, and does this three times:

Once again Steven's Dad puts him back at the start, but facing the other way. Steven takes 2 steps forward (for him!) but he is heading in the negative direction. He does this 3 times:

Back at the start again (thanks Dad!), still facing in the negative direction, he tries his backwards walking, once again taking two steps at a time, and he does this three times:

So, by walking backwards, while facing in the negative direction, he moves in the positive direction.

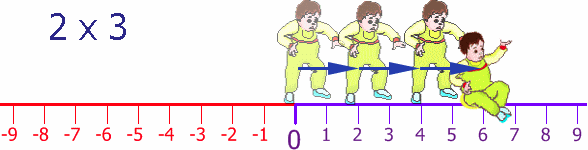
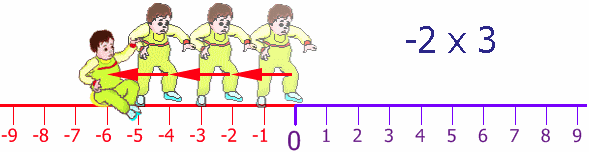
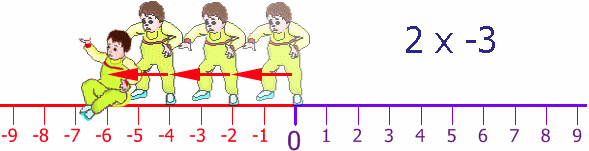
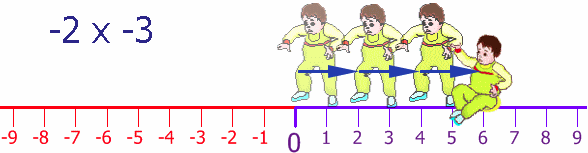
Try it yourself! Try walking forwards and backwards, then again but facing the other direction.

Multiplying Positive And Negative Numbers

When you have finished this page, try the Multiplying Positive and Negative Numbers Quiz.   (Click the link to take the quiz)
http://www.mcwdn.org/Algebra/MultPosNeg.html

The multiplication of positive and negative numbers has certain rules depending on the equation. Let's take a look at an example with positive numbers and the number line. You notice that the ball goes from the starting point zero to five, then ten, then fifteen as five times three is fifteen.

In this example, negative five is multiplied by three. Notice that this time the ball goes to the left five, then ten, then fifteen. A negative five times three or three times a negative five is a negative fifteen.

The next case is a bit trickier to understand. A negative five is multiplied by a negative three with an answer of a positive fifteen. This is because each time the negative five is multiplied by another negative number, it is as such changing the negative to a positive - taking away each time a negative and changing the number to a positive.

Multiplying Rules:
Positive x Positive = Positive: 3 x 2 = 6
Negative x Negative = Positive: (-2) x (-8) = 16
Negative x Positive = Negative: (-3) x 4 = -12
Positive x Negative = Negative: 3 x (-4) = -12

You can play this multiplication game using Negative and Positive number.
Click the link to play the game
http://primarygamesarena.com/Multiplying-Negative-Numbers410 Negative number multiplication game

LESSON PRACTICE
Multiply.
 1. (+5) x (–6) =
2. (–6) x (–7) =
 3. (–9) x (–10) =
4. (–10) x (+12) =
 5. (–5) x (–8) =
 6. (–16) x (–11) =
 7. (+4) x (–15) =
8. (–18) x (–6) =
 9. (–16) x (+12) =
 10. (–17) x (+3) =
 11. (–18) x (–4) =
12. (–24) x (–5) =

Documentation of Sources: 
Definition: Mathmatics for Elementary Teacher Beckmann, Sybilla
Concept meaning:  http://www.mathsisfun.com/multiplying-negatives.html
Using a Number Line: http://www.mathsisfun.com/multiplying-negatives.html
Multiplying Neg Numbers with Quiz: http://www.mcwdn.org/Algebra/MultPosNeg.html

Common Core Standards 
The Number System (NS) Apply and extend previous understandings of operations with fractions to add, subtract, multiply, and divide rational numbers. Standards Mathematical Practices Explanations and Examples Students are expected to:   7.NS.2. Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers.
 a. Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as (–1)(–1) = 1 and the rules for multiplying signed numbers. Interpret products of rational numbers by describing real-world contexts. 
b. Understand that integers can be divided, provided that the divisor is not zero, and every quotient of integers (with non-zero divisor) is a rational number. If p and q are integers, then –(p/q) = (–p)/q = p/(–q). Interpret quotients of rational numbers by describing real-world contexts. 
c. Apply properties of operations as strategies to multiply and divide rational numbers. 
d. Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0s or eventually repeats.   7
.MP.2. Reason abstractly and quantitatively. 
 7.MP.4. Model with mathematics.  
7.MP.7. Look for and make use of structure. Multiplication and division of integers is an extension of multiplication and division of whole numbers.  
 Examples: • Examine the family of equations. What patterns do you see? Create a model and context for each of the products. Write and model the family of equations related to 3 x 4 = 12.  Equation Number Line Model Context 2 x 3 = 6    Selling two packages of apples at $3.00 per pack 2 x -3 = -6  Spending 3 dollars each on 2 packages of apples -2 x 3 = -6     Owing 2 dollars to each of your three friends -2 x -3 = 6       Forgiving 3 debts of $2.00 each